еӣҪе·Ҙж•°жҚ®еӨ§и„‘д№ӢеӨҡе…ғзәҝжҖ§еӣһеҪ’еңЁеҢ–еӯҰз ”еҸ‘дёӯйў„жөӢзҡ„еә”з”Ё
дҪңиҖ…пјҡеӣҪе·ҘжҷәиғҪз ”еҸ‘йғЁ—йҷҲжёқж•Ҹ
дёҡеҠЎиғҢжҷҜ
дёҚз®ЎжҳҜеҲ¶йҖ дёҡиҝҳжҳҜеҢ–е·ҘиЎҢдёҡпјҢеҜ№дәҺжҲҗжң¬жҲ–дә§йҮҸжҺ§еҲ¶гҖҒйў„жөӢгҖҒеҶізӯ–йғҪжҳҜз”ҹдә§з®ЎзҗҶдёӯзҡ„йҮҚиҰҒз»„жҲҗйғЁеҲҶгҖӮд»ҘжҲҗжң¬жҺ§еҲ¶дёәдҫӢпјҢиҝҮеҺ»дәә们еҜ№жҲҗжң¬жҺ§еҲ¶зҡ„и®ӨиҜҶжҜ”иҫғзӢӯйҡҳпјҢдј з»ҹзҡ„жҲҗжң¬жҺ§еҲ¶иҢғеӣҙеұҖйҷҗдәҺеҲ¶йҖ дә§е“Ғзҡ„иҝҮзЁӢпјҢдҫӢеҰӮеҜ№жҲҗжң¬еҪўжҲҗиҝҮзЁӢдёӯдёҖдәӣиҖ—иҙ№жҢҮж Үзҡ„жҺ§еҲ¶пјҢдҪҝе®ғдёҚи¶…иҝҮе®ҡйўқйў„з®—пјҢеҰӮжһңеҸ‘з”ҹе·®ејӮпјҢиҝӣиЎҢе·®ејӮи®Ўз®—е’Ңе·®ејӮеҲҶжһҗпјҢд»ҘиҫҫеҲ°йҷҚдҪҺжҲҗжң¬зҡ„зӣ®зҡ„гҖӮжүҖд»Ҙ,дј з»ҹжҲҗжң¬жҺ§еҲ¶йҮҚзӮ№еңЁз”ҹдә§иҝҮзЁӢдёӯзҡ„е·®ејӮи®Ўз®—е’Ңз»“жқҹз”ҹдә§иҝҮзЁӢеҗҺзҡ„е·®ејӮеҲҶжһҗпјҢжҳҜдёҖз§Қж¶ҲжһҒзҡ„жҲҗжң¬жҺ§еҲ¶гҖӮеҗҢж—¶пјҢдјҒдёҡиҖ—иҙ№еӨ§йҮҸдәәеҠӣпјҢзү©еҠӣ收йӣҶзҡ„ж•°жҚ®еҸҠжҢҮж ҮдҝЎжҒҜ并没жңүеҫ—еҲ°еҫҲеҘҪзҡ„еҲ©з”ЁпјҢеҸӘжҳҜеҒңз•ҷеңЁиЎЁйқўзҡ„еҲҶжһҗгҖӮиҖҢеҖҹеҠ©еӣҪе·Ҙж•°жҚ®еӨ§и„‘е№іеҸ°зҡ„еӨҡе…ғзәҝжҖ§еӣһеҪ’еҲҶжһҗз®—жі•пјҢдёҚдҪҶеҸҜд»ҘеҒҡеҲ°еҜ№жҲҗжң¬зҡ„дәӢе…ҲжҺ§еҲ¶пјҢеҚіеҜ№дјҒдёҡжңӘжқҘеҮ е№ҙзҡ„жҲҗжң¬иҝӣиЎҢйў„жөӢпјҢиҝҳеҸҜд»ҘеҸҠж—©еҸ‘зҺ°дјҒдёҡжҠ•е…Ҙзҡ„жҲҗжң¬дёҚи¶іжҲ–жҲҗжң¬иҝҮеү©зҡ„зҺ°иұЎпјҢеё®еҠ©з»„з»ҮжҳҺзЎ®жңӘжқҘжҲҗжң¬йңҖжұӮи¶ӢеҠҝпјҢеҒҡеҘҪжҲҗжң¬и§„еҲ’е·ҘдҪңпјҢд»ҺиҖҢиҝӣиЎҢеҮҶзЎ®еҶізӯ–пјӣиҖҢдё”еҸҜд»ҘеӨҚз”ЁеҺҶеҸІжҲҗжң¬ж•°жҚ®ж·ұеәҰжҢ–жҺҳеҮәжңүз”Ёзҡ„дҝЎжҒҜпјҢжҺўзҙўеҮәе…·жңүдёҖиҲ¬и§„еҫӢжҖ§е’Ңжҷ®йҒҚйҖӮз”ЁжҖ§зҡ„жҲҗжһңгҖӮ
еӨҡе…ғзәҝжҖ§еӣһеҪ’е®ҡд№ү
еӣһеҪ’еҲҶжһҗжҳҜдҪңдёәж•°жҚ®з§‘еӯҰ家йңҖиҰҒжҺҢжҸЎзҡ„第дёҖдёӘз®—жі•пјҢжҳҜж•°жҚ®еҲҶжһҗдёӯжңҖеҹәзЎҖжңҖйҮҚиҰҒзҡ„еҲҶжһҗе·Ҙе…·пјҢз»қеӨ§еӨҡж•°зҡ„ж•°жҚ®еҲҶжһҗй—®йўҳпјҢйғҪеҸҜд»ҘдҪҝз”ЁеӣһеҪ’зҡ„жҖқжғіжқҘи§ЈеҶігҖӮеӣһеҪ’еҲҶжһҗзҡ„д»»еҠЎе°ұжҳҜпјҢйҖҡиҝҮз ”з©¶иҮӘеҸҳйҮҸXе’Ңеӣ еҸҳйҮҸYзҡ„ж•°еӯҰе…ізі»ејҸиҝӣиҖҢиҫҫеҲ°йҖҡиҝҮXеҺ»йў„жөӢYзҡ„зӣ®зҡ„пјҢе®ғжҳҜж•°жҚ®еҲҶжһҗдёӯжңҖеёёз”Ёзҡ„йў„жөӢе»әжЁЎжҠҖжңҜд№ӢдёҖгҖӮеҚідҪҝеңЁд»ҠеӨ©пјҢеӨ§еӨҡж•°е…¬еҸёйғҪдҪҝз”ЁеӣһеҪ’жҠҖжңҜжқҘе®һзҺ°еӨ§и§„жЁЎеҶізӯ–гҖӮе…¶дёӯеҢ…жӢ¬дәҶдёҖе…ғзәҝжҖ§еӣһеҪ’ж–№жі•гҖҒеӨҡе…ғзәҝжҖ§еӣһеҪ’ж–№жі•е’ҢйқһзәҝжҖ§еӣһеҪ’ж–№жі•зӯүгҖӮпјҲзәҝжҖ§жҢҮзҡ„жҳҜXгҖҒYд№Ӣй—ҙе‘ҲзәҝжҖ§е…ізі»пјҢдёҚз®ЎXеҸ–д»Җд№ҲеҖјпјҢйғҪиғҪеңЁиҝҷжқЎеӣһеҪ’зӣҙзәҝдёҠжүҫеҲ°еҜ№еә”зҡ„YпјҢеҰӮеӣҫ1пјҢеҸӘиҰҒиҫ“е…ҘX,Yзҡ„ж ·жң¬ж•°жҚ®пјҢж•°жҚ®еӨ§и„‘дёӯзҡ„жӢҹеҗҲеӣһеҪ’з®—жі•е°ұиғҪеҫ—еҲ°зӣёеә”зҡ„еӣһеҪ’зӣҙзәҝпјү
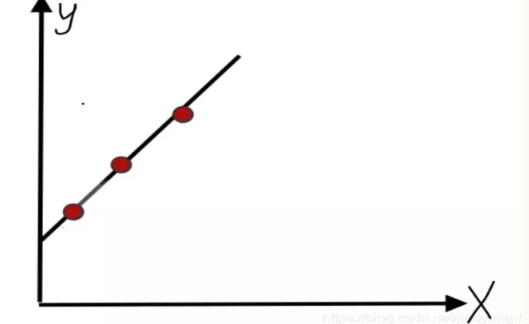
еӣҫ1
з•Ңе®ҡзәҝжҖ§еӣһеҪ’жҳҜеҗҰдёәеӨҡе…ғпјҢдё»иҰҒзңӢиҮӘеҸҳйҮҸпјҲеҚіXпјүзҡ„дёӘж•°,иӢҘиҮӘеҸҳйҮҸдёӘж•°еңЁдёӨдёӘеҸҠе…¶д»ҘдёҠпјҢеҲҷз§°е…¶дёәеӨҡе…ғзәҝжҖ§еӣһеҪ’пјҢжҳҫ然иӢҘиҮӘеҸҳйҮҸдёӘж•°жңүдё”еҸӘжңүдёҖдёӘпјҢз§°дёәдёҖе…ғзәҝжҖ§еӣһеҪ’гҖӮеӨҡе…ғзәҝжҖ§еӣһеҪ’зҡ„еҹәжң¬еҺҹзҗҶе’ҢдёҖе…ғзәҝжҖ§еӣһеҪ’е®Ңе…ЁзӣёеҗҢпјҢеҢәеҲ«еҸӘеңЁдәҺиҮӘеҸҳйҮҸзҡ„дёӘж•°гҖӮ
еңЁе®һйҷ…дёӯпјҢдёҖдёӘжҢҮж Үзҡ„еҪұе“Қеӣ зҙ йҖҡеёёдёҚжӯўдёҖдёӘпјҢиҖҢжҳҜжңүиӢҘе№ІдёӘйҮҚиҰҒеӣ зҙ е…ұеҗҢдҪңз”ЁжүҚеҜјиҮҙдәӢзү©зҡ„еҸ‘еұ•еҸҳеҢ–,еӣ жӯӨеңЁе®һйҷ…еҲҶжһҗж—¶еӨҡиҖғиҷ‘еӨҡе…ғеӣһеҪ’еҲҶжһҗпјҢжң¬ж–Үд»ҘиҫғдёәеӨҚжқӮзҡ„еӨҡе…ғзәҝжҖ§еӣһеҪ’дёәдҫӢгҖӮеӨҡе…ғзәҝжҖ§еӣһеҪ’жЁЎеһӢзҡ„дёҖиҲ¬еҪўејҸдёәпјҡ
Y=a0+a1*X1+a2*X2+a3*X3…
YжҢҮзҡ„жҳҜеӣ еҸҳйҮҸпјҢеҚіжҲ‘们关注зҡ„жҢҮж ҮпјҲжҲҗжң¬жҲ–дә§йҮҸзӯүпјүпјӣXжҢҮзҡ„жҳҜеҪұе“ҚYзҡ„еӣ зҙ гҖӮa1,a2,a3……жҢҮзҡ„жҳҜеҪұе“ҚзЁӢеәҰзҡ„еӨ§е°ҸпјҲеҸҲз§°еӣһеҪ’зі»ж•°еӨ§е°ҸпјүгҖӮ
еӣһеҪ’еҲҶжһҗзҡ„еә”з”Ё
еӣһеҪ’еҲҶжһҗз”ЁдәҺеңЁи®ёеӨҡдёҡеҠЎжғ…еҶөдёӢеҒҡеҮәеҶізӯ–гҖӮеӣһеҪ’еҲҶжһҗжңүдёүдёӘдё»иҰҒеә”з”Ё:
1.и§ЈйҮҠдјҒдёҡзҗҶи§Јеӣ°йҡҫзҡ„дәӢжғ…гҖӮдҫӢеҰӮпјҢдёәд»Җд№ҲеңЁдёҠдёҖеӯЈеәҰзҡ„иҗҘдёҡйўқжңүжүҖдёӢйҷҚгҖӮ
2.йў„жөӢйҮҚиҰҒзҡ„е•Ҷдёҡи¶ӢеҠҝгҖӮдҫӢеҰӮпјҢжҳҺе№ҙдјҡиҰҒжұӮ他们зҡ„дә§е“ҒзңӢиө·жқҘеғҸд»Җд№Ҳ?
3.йҖүжӢ©дёҚеҗҢзҡ„жӣҝд»Јж–№жЎҲгҖӮдҫӢеҰӮпјҢжҲ‘们еә”иҜҘйҖүжӢ©еҺҹж–ҷAиҝҳжҳҜеҺҹж–ҷB?
иҝӣиЎҢйў„жөӢзҡ„еүҚжҸҗ
еҪ“жҲ‘们жұӮеҮәеӣһеҪ’жЁЎеһӢзҡ„е…·дҪ“иЎЁиҫҫејҸж—¶пјҢиҝҳйңҖиҰҒиҝӣиЎҢз»ҹи®Ўж„Ҹд№үжЈҖйӘҢпјҢйҖҡиҝҮжЈҖйӘҢжүҚиғҪдҪҝз”ЁиҜҘжЁЎеһӢиҝӣиЎҢйў„жөӢгҖӮдё»иҰҒеҢ…жӢ¬:жӢҹеҗҲдјҳеәҰжЈҖйӘҢгҖҒеӣһеҪ’жЁЎеһӢзҡ„жҖ»дҪ“жҳҫи‘—жҖ§жЈҖйӘҢе’ҢеӣһеҪ’зі»ж•°зҡ„жҳҫи‘—жҖ§жЈҖйӘҢзӯүгҖӮ
1. жӢҹеҗҲдјҳеәҰжЈҖйӘҢ
жӢҹеҗҲдјҳеәҰжҳҜжҢҮжӢҹеҗҲзҡ„еӣһеҪ’жЁЎеһӢдёҺж ·жң¬и§ӮжөӢеҖјд№Ӣй—ҙзҡ„жҺҘиҝ‘зЁӢеәҰгҖӮеҚіиЎЎйҮҸдёҖдёӘеӣһеҪ’жЁЎеһӢеҒҡзҡ„еҘҪдёҚеҘҪзҡ„жҢҮж ҮгҖӮз”ЁеҶіе®ҡзі»ж•°пјҲR-sqпјүиЎЁзӨәпјҢе…¶ж•°еҖјеҢәй—ҙдёә 0 —— 1пјҢи¶ҠжҺҘиҝ‘1пјҢиҜҙжҳҺжЁЎеһӢжӢҹеҗҲеҫ—и¶ҠеҘҪгҖӮеҲӨж–ӯж ҮеҮҶдёәпјҡеӨ§дәҺжҲ–зӯүдәҺ0.7пјҢи®ӨдёәжӢҹеҗҲдјҳеәҰиҫғеҘҪпјӣеңЁ0.35——0.7д№Ӣй—ҙпјҢи®ӨдёәжӢҹеҗҲдјҳеәҰиҫғжҷ®йҖҡпјӣе°ҸдәҺ0.35пјҢи®ӨдёәжӢҹеҗҲдјҳеәҰиҫғе·®гҖӮ
2.еӣһеҪ’ж–№зЁӢзҡ„жҳҫи‘—жҖ§жЈҖйӘҢ
еҚіжЈҖйӘҢж•ҙдёӘеӣһеҪ’ж–№зЁӢзҡ„жҳҫи‘—жҖ§пјҢжҲ–иҖ…иҜҙиҜ„д»·жүҖжңүиҮӘеҸҳйҮҸxж•ҙдҪ“дёҺеӣ еҸҳйҮҸYзҡ„зәҝжҖ§е…ізі»жҳҜеҗҰеҜҶеҲҮпјҢж•ҙдёӘеӣһеҪ’ж–№зЁӢжң¬иә«жҳҜеҗҰжңүж•ҲгҖӮйҖҡеёёйҮҮз”ЁFжЈҖйӘҢгҖӮ
3.еӣһеҪ’зі»ж•°зҡ„жҳҫи‘—жҖ§
иӢҘж–№зЁӢйҖҡиҝҮжҳҫи‘—жҖ§жЈҖйӘҢпјҢ并дёҚж„Ҹе‘ізқҖжҜҸдёӘиҮӘеҸҳйҮҸеҜ№yзҡ„еҪұе“ҚйғҪжҳҫи‘—пјҢжүҖд»Ҙе°ұйңҖиҰҒжҲ‘们еҜ№жҜҸдёӘиҮӘеҸҳйҮҸиҝӣиЎҢжҳҫи‘—жҖ§жЈҖйӘҢгҖӮиӢҘжҹҗдёӘиҮӘеҸҳйҮҸзі»ж•°еҜ№yеҪұе“ҚдёҚжҳҫи‘—пјҢеҚіж— е…ізҡ„еҸҳйҮҸгҖӮжҲ‘们йңҖиҰҒд»ҺеӣһеҪ’ж–№зЁӢдёӯе°Ҷе…¶еү”йҷӨгҖӮйҖҡеёёйҮҮз”ЁtжЈҖйӘҢгҖӮ
еә”з”ЁеңәжҷҜ
жҲҗжң¬й«ҳдҪҺдёҚд»…еҪұе“ҚзқҖеҢ–е·ҘиЎҢдёҡдјҒдёҡзҡ„еҲ©ж¶ҰпјҢжӣҙжҳҜе…¶е…¬еҸёеҸ‘еұ•еЈ®еӨ§зҡ„дёҖдёӘеҲ¶зәҰеӣ зҙ гҖӮжҹҗжңүжңәж–°жқҗж–ҷдјҒдёҡжғіиҰҒеҮҸе°‘еҢ–еӯҰеҸҚеә”дёӯзҡ„еҺҹж–ҷеү©дҪҷ并预жөӢеңЁжҹҗз§ҚеҸҚеә”еҸӮж•°еҸҳйҮҸеҸ–еҖјдёӢзҡ„еҺҹж–ҷеү©дҪҷгҖӮеҺҹж–ҷеү©дҪҷи¶Ҡе°‘пјҢжҲҗжң¬еҲ©з”ЁзҺҮи¶Ҡй«ҳгҖӮжҠҠжҲ‘们жғіиҰҒз ”з©¶зҡ„еҜ№иұЎеҺҹж–ҷеү©дҪҷпјҲYпјүдҪңдёәеӣ еҸҳйҮҸпјҢйҖүеҸ–дәҶ4дёӘдё»иҰҒеҪұе“Қеӣ зҙ пјҡеҺҹж–ҷAзҡ„SM(X1)пјӣеҺҹж–ҷBзҡ„зЎқй…ёпјҲX2пјү;жё©еәҰ(X3);еҸҚеә”ж—¶й—ҙпјҲX4пјүгҖӮ并иҝӣиЎҢ22ж¬ЎиҜ•йӘҢгҖӮеҹәдәҺ22ж¬Ўе®һйӘҢж•°жҚ®иҝӣиЎҢеӨҡе…ғзәҝжҖ§еӣһеҪ’гҖӮ
еҲқжӯҘеҫ—еҲ°зәҝжҖ§еӣһеҪ’ж–№зЁӢпјҡY=a0+a1*X1+a2*X2+a3*X3+a4*X4гҖӮ
йҰ–е…ҲпјҢеҲ©з”Ёж•°жҚ®еӨ§и„‘дёӯзҡ„еӨҡе…ғзәҝжҖ§еӣһеҪ’组件пјҢе°ұеҸҜеҫ—еҲ°еӣһеҪ’зі»ж•°пјҡa1,a2,a3,a4зҡ„еҖјгҖӮеҚіжҠҠеӨҡе…ғзәҝжҖ§еӣһеҪ’组件жӢ–еҲ°еҲ°е·ҘдҪңйқўжқҝпјҢй…ҚзҪ®ж•°жҚ®еҸҠ组件еҸӮж•°пјҡе°Ҷеӣ еҸҳйҮҸе’Ң4дёӘиҮӘеҸҳйҮҸеҲҶеҲ«жӢ–еҲ°еҜ№еә”зҡ„еҢәеҹҹгҖӮиҝҮзЁӢеҰӮеӣҫ1пјҡ

еӣҫ1
й…ҚзҪ®еҘҪеҸӮж•°д№ӢеҗҺпјҢе…¶ж¬ЎзӮ№еҮ»иҝҗиЎҢпјҢз»“жһңеҰӮдёӢпјҡ
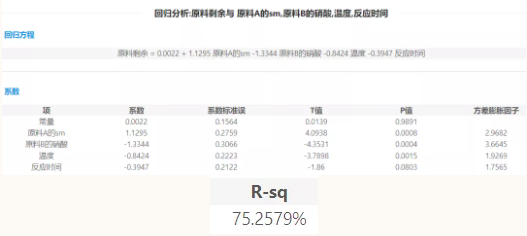
еӣҫ2

еӣҫ3
з”ұеӣҫ2еҸҜзҹҘпјҢе…ідәҺжӢҹеҗҲдјҳеәҰжЈҖйӘҢж–№йқўпјҢеҶіе®ҡзі»ж•°R-sq(еҚіRж–№)=0.7526пјҢиҜҙжҳҺиҜҘжЁЎеһӢжӢҹеҗҲдјҳеәҰиҫғеҘҪпјҢеӣ еҸҳйҮҸYдёҺиҮӘеҸҳйҮҸX1,X2,X3,X4е…·жңүиҫғй«ҳзҡ„зәҝжҖ§зӣёе…іе…ізі»гҖӮ
д»Һеӣҫ3еҸҜзҹҘпјҡеҜ№дәҺFжЈҖйӘҢпјҢжҹҘFеҲҶеёғиЎЁеҸҜзҹҘпјҢжҳҫи‘—жҖ§ж°ҙе№ідёә0.1жүҖеҜ№еә”зҡ„Fдёҙз•ҢеҖјжҳҜ2.31пјҢFжЈҖйӘҢз»ҹи®ЎйҮҸзҡ„еҖјдёә5.5пјҢж•…Fз»ҹи®ЎйҮҸзҡ„еҖј>дёҙз•ҢеҖј,жӢ’з»қеҺҹеҒҮи®ҫгҖӮиҜҙжҳҺж•ҙдёӘеӣһеҪ’жЁЎеһӢжҳҜжңүж•Ҳзҡ„пјҢжүҖжңүиҮӘеҸҳйҮҸж•ҙдҪ“еҜ№YжңүеҪұе“ҚгҖӮ
еҜ№дәҺtжЈҖйӘҢпјҢз”ұеӣҫ2 жҳҫзӨәпјҢеңЁ0.1зҡ„жҳҫи‘—жҖ§ж°ҙе№ідёӢпјҢеӣӣдёӘиҮӘеҸҳйҮҸзҡ„pеҖјеҲҶеҲ«дёәпјҡp1=0008;p2=0.004;p3=0.0015;p4=0.0803пјҢеқҮе°ҸдәҺ0.1пјҢж•…жӢ’з»қеҺҹеҒҮи®ҫпјҢиҝӣдёҖжӯҘиЎЁжҳҺжҜҸдёҖдёӘиҮӘеҸҳйҮҸеҜ№Yжңүжҳҫи‘—еҪұе“ҚгҖӮз»јдёҠпјҢжүҖжңүз»“жһңжҳҫзӨәжӯӨеӣһеҪ’жЁЎеһӢйҖҡиҝҮдәҶз»ҹи®Ўж„Ҹд№үзҡ„жЈҖйӘҢпјҢиҜҙжҳҺжӯӨеӣӣе…ғзәҝжҖ§еӣһеҪ’жЁЎеһӢжҳҜжҲҗз«Ӣзҡ„пјҢеҸҜд»Ҙз”ЁдәҺйў„жөӢгҖӮ
е·ІзҹҘa1=1.130,a2=-1.334;a3=-0.842;a4=-0.395гҖӮ
жңҖз»Ҳзҡ„еӨҡе…ғзәҝжҖ§еӣһеҪ’ж–№зЁӢдёәпјҡY=0.002+1.1295 X1-1.3344 X2-0.8424X3-0.395 X4
жӯӨж–№зЁӢзҡ„ж„Ҹд№үжҳҜ:еңЁеҒҮе®ҡе…¶е®ғиҮӘеҸҳйҮҸдёҚеҸҳзҡ„жғ…еҶөдёӢпјҢеҺҹж–ҷAзҡ„SMпјҲX1пјүжҜҸеўһй•ҝ1gпјҢеҺҹж–ҷеү©дҪҷе°ұеўһй•ҝ1.1295gпјӣеңЁеҒҮе®ҡе…¶е®ғиҮӘеҸҳйҮҸдёҚеҸҳзҡ„жғ…еҶөдёӢпјҢеҺҹж–ҷBзҡ„зЎқй…ё(X2)жҜҸеўһй•ҝ1gпјҢеҺҹж–ҷеү©дҪҷе°ұеҮҸе°‘1.3344gпјӣеңЁеҒҮе®ҡе…¶е®ғиҮӘеҸҳйҮҸдёҚеҸҳзҡ„жғ…еҶөдёӢпјҢжё©еәҰпјҲX3пјүжҜҸжҸҗй«ҳ1ж‘„ж°ҸеәҰпјҢеҺҹж–ҷеү©дҪҷе°ұеҮҸе°‘0.8424gпјӣеңЁеҒҮе®ҡе…¶е®ғеҸҳйҮҸдёҚеҸҳзҡ„жғ…еҶөдёӢпјҢеҸҚеә”ж—¶й—ҙпјҲX4пјүжҜҸжҸҗй«ҳ1з§’пјҢеҺҹж–ҷеү©дҪҷе°ұеҮҸе°‘0.395gпјӣеҗҢж—¶пјҢеӣһеҪ’зі»ж•°aзҡ„з»қеҜ№еҖји¶ҠеӨ§пјҢеҜ№Yзҡ„еҪұе“Қи¶ҠеӨ§пјҢеҸҜд»ҘзңӢеҮәa2зҡ„з»қеҜ№еҖјжңҖеӨ§пјҢдёә1.334гҖӮеңЁеҶізӯ–ж–№йқўпјҢиӢҘиҜҘдјҒдёҡжғіеҮҸе°‘еҺҹж–ҷеү©дҪҷзҺҮпјҢеә”еҪ“еӨҡе…іжіЁеҺҹж–ҷBзҡ„жғ…еҶөгҖӮ
еңЁйў„жөӢж–№йқўпјҡиӢҘдёӢдёҖж¬Ўе®һйӘҢж—¶пјҢеҒҮи®ҫX1=1.260пјҢX2=-0.371пјҢX3=-0.670пјӣX4=0.770пјҢеҲҷYзҡ„йў„жөӢеҖј=0.002+1.1295*1.260-1.3344*пјҲ-0.371пјү-0.8424*пјҲ-0.670пјү-0.3947*0.770=2.179пјҲgпјүгҖӮеҚіеҺҹж–ҷеү©дҪҷдёә2.179g,иҜҘдјҒдёҡеҸҜд»Ҙе°Ҷе…¶дёҺдёҠдёҖж¬Ўе®һйӘҢиҝӣиЎҢжҜ”иҫғпјҢд»ҺиҖҢиҝӣиЎҢзӣёеә”зҡ„еҶізӯ–гҖӮ

еӣҪе·ҘжҷәиғҪжҳҜдёҖ家专дёҡдёәжөҒзЁӢеҲ¶йҖ дёҡжҸҗдҫӣдәәе·ҘжҷәиғҪеҶізӯ–жҺ§еҲ¶ж•ҙдҪ“и§ЈеҶіж–№жЎҲеҸҠиҗҪең°жңҚеҠЎзҡ„еӣҪжңүеҸӮиӮЎй«ҳж–°жҠҖжңҜдјҒдёҡпјҢдё“жіЁдәҺеҲ©з”Ёдәәе·ҘжҷәиғҪгҖҒеӨ§ж•°жҚ®зӯүжҠҖжңҜи§ЈеҶіжөҒзЁӢеҲ¶йҖ дёҡжө·йҮҸж•°жҚ®дёӢеӨҚжқӮеңәжҷҜзҡ„жҷәиғҪеҲ¶йҖ йңҖжұӮпјҢдёәе®ўжҲ·жҸҗдҫӣ“IOT+AI+OR”жҷәиғҪеҲ¶йҖ дәәе·ҘжҷәиғҪж•ҙдҪ“и§ЈеҶіж–№жЎҲгҖӮзӣ®еүҚпјҢе…¬еҸёе·Із»ҸжҲҗдёәеҢ–е·Ҙж–°жқҗж–ҷиЎҢдёҡдәәе·ҘжҷәиғҪеҶізӯ–жҺ§еҲ¶йўҶеҹҹзҡ„йўҶи·‘иҖ…гҖӮ
дҪңдёәдёҖ家еӣҪеҶ…дё“дёҡзҡ„жҷәиғҪеҲ¶йҖ иҗҪең°жңҚеҠЎе•ҶпјҢеӣҪе·ҘжҷәиғҪеҮӯеҖҹж·ұеҺҡзҡ„еҶ…еҠҹе’Ңдјҳз§Җзҡ„еӣўйҳҹпјҢиҮӘдё»з ”еҸ‘дәҶеҹәдәҺдәәе·ҘжҷәиғҪзҡ„ж•°жҚ®еӨ§и„‘еҲҶжһҗе№іеҸ°(MAI)гҖҒжҷәиғҪеҲ¶йҖ з®ЎзҗҶе№іеҸ°пјҲMESпјүгҖҒзү©иҒ”зҪ‘ж•°жҚ®йҮҮйӣҶе№іеҸ°пјҲSCADAпјүгҖҒе®һйӘҢе®Өз®ЎзҗҶзі»з»ҹпјҲLIMSпјүгҖҒеҸҢдҪ“зі»и®ҫеӨҮз®ЎзҗҶзі»з»ҹпјҲEMSпјүпјҢеқҮеңЁиЎҢдёҡеҶ…жҲҗеҠҹеә”з”ЁгҖӮ

еӣҪе·ҘжҷәиғҪеңЁеҢ–е·ҘгҖҒеҢ»иҚҜгҖҒйЈҹе“ҒгҖҒйҘІж–ҷгҖҒж–°жқҗж–ҷзӯүиЎҢдёҡж·ұиҖ•е·Ід№…пјҢе®ўжҲ·йҒҚеёғе…ЁеӣҪпјҢе·ІжҲҗеҠҹдёәжө·еӨ§йӣҶеӣўгҖҒеҚҺж¶Ұдёүд№қиҚҜдёҡгҖҒеә·зјҳиҚҜдёҡгҖҒдё°еҺҹйӣҶеӣўгҖҒйҒ“жҒ©йӣҶеӣўгҖҒд№қзӣ®еҢ–еӯҰгҖҒи“қеёҶеҢ»з–—гҖҒж–°ж—¶д»ЈеҒҘеә·дә§дёҡйӣҶеӣўгҖҒе®ү然зәізұійӣҶеӣўзӯүе®ўжҲ·жҸҗдҫӣжҷәиғҪеҲ¶йҖ иҗҪең°жңҚеҠЎгҖӮ

еӣҪе·ҘжҷәиғҪз§үжүҝ“еҲ©дәҺеӣҪпјҢзІҫдәҺе·Ҙ”зҡ„дјҒдёҡеҸ‘еұ•зҗҶеҝөпјҢд»Ҙй«ҳз«ҜITжҠҖжңҜжңҚеҠЎдәҺдј з»ҹеҲ¶йҖ дјҒдёҡпјҢжҺЁеҠЁеӣҪ家еҲ¶йҖ дёҡиҪ¬еһӢеҚҮзә§пјҢд»Ҙе·ҘеҢ зІҫзҘһдёәдёӯеӣҪжҷәйҖ иөӢиғҪпјҒеҠӘеҠӣжҲҗдёә科жҠҖеҲӣж–°е’Ңдә§дёҡйқ©е‘Ҫзҡ„еј•йўҶиҖ…пјҢдёәдёӯеӣҪе®һдҪ“з»ҸжөҺеҙӣиө·гҖҒе®һзҺ°дёӯеӣҪеҲ¶йҖ 2025иҙЎзҢ®еҠӣйҮҸпјҒ

еӣҪе·Ҙж•°жҚ®еӨ§и„‘зі»з»ҹпјҲMAI-CLIпјүжҳҜдёҖдёӘйӣҶж•°жҚ®и°ғеәҰпјҢж•°жҚ®жё…жҙ—пјҢж•°жҚ®и®Ўз®—гҖҒж•°жҚ®еҸҜи§ҶеҢ–зҡ„ж•°жҚ®еҲҶжһҗе№іеҸ°гҖӮзі»з»ҹд»Ҙз®ҖеҚ•жҳ“з”ЁжӢ–еҠЁж“ҚдҪңж–№ејҸиҝӣиЎҢдәәжңәдәӨдә’пјҢеұҸи”ҪдәҶж•°жҚ®еҲҶжһҗйў„жөӢдёҡеҠЎзҡ„еӨҚжқӮжҖ§пјҢеӨ§еӨ§йҷҚдҪҺдәҶж•°жҚ®еҲҶжһҗе·ҘдҪңзҡ„жҠҖжңҜй—Ёж§ӣгҖӮ
д»Ҙи®Ўз®—жөҒзҡ„ж–№ејҸжһ„е»әж•ҙдёӘж•°жҚ®еҲҶжһҗдёҡеҠЎгҖӮе№іеҸ°е®һзҺ°дәҶеҜ№еҲҶж•Јзҡ„ж•°жҚ®иҝӣиЎҢз»ҹдёҖи°ғеәҰпјҢе®һзҺ°е®һйӘҢе®Өи®ҫеӨҮгҖҒе·Ҙдёҡдј ж„ҹеҷЁгҖҒдҝЎжҒҜеҢ–зі»з»ҹжҺҘеҸЈеӨҡжәҗж•°жҚ®ж•ҙеҗҲгҖӮ
е№іеҸ°жҸҗдҫӣдёҠзҷҫдёӘеҠҹиғҪ组件пјҢеҢ…еҗ«ж–№е·®гҖҒеӣһеҪ’гҖҒиҒҡзұ»гҖҒеҲҶзұ»гҖҒж—¶й—ҙеәҸеҲ—зӯү算法组件пјҢж”ҜжҢҒSPCгҖҒDOEгҖҒCPKгҖҒMSAзӯүеҲҶжһҗзҗҶеҝөпјҢе№іеҸ°жӢҘжңүе®ҡж—¶еҲҶжһҗеҠҹиғҪпјҢеҸҜд»ҘеҗҢж—¶зӣ‘жҺ§дёҠдёҮзҡ„иҙЁйҮҸзӣ‘жҺ§зӮ№гҖӮиғҪе®һзҺ°иҮӘеҠЁеҢ–е…ӯиҘҝж јзҺӣе®һж–ҪиҗҪең°гҖӮ
еә”з”ЁеңәжҷҜ
и®ЎеҲ’з»ҸзҗҶеҸҜд»Ҙз”ЁжқҘйў„жөӢжңӘжқҘй”Җе”®жғ…еҶөпјҢ并иҮӘеҠЁи·ҹиёӘжү§иЎҢгҖӮ
иҙЁйҮҸз»ҸзҗҶеҸҜд»Ҙз”ЁжқҘеҒҡSPCеҲҶжһҗгҖҒеҸ–ж ·е·®ејӮгҖҒж–№е·®еҲҶжһҗгҖӮ
з ”еҸ‘з»ҸзҗҶеҸҜд»ҘеҒҡй…Қж–№дјҳеҢ–йў„жөӢгҖҒе®һйӘҢиҫ…еҠ©и®ҫи®ЎгҖҒе·ҘиүәеҲҶжһҗгҖҒж•°жҚ®д»ҝзңҹгҖӮ
и®ҫеӨҮз»ҸзҗҶеҸҜд»Ҙз”ЁжқҘеҒҡи®ҫеӨҮйў„жөӢжҖ§з»ҙжҠӨгҖҒжҠҘиӯҰгҖӮ
е№іеҸ°е·Із»Ҹе®ҢжҲҗиҫ№зјҳи®Ўз®—е°ҒиЈ…пјҢеҸҜд»ҘдёҺи®ҫеӨҮиҝӣиЎҢдә’еҠЁгҖӮ
еҗҢж—¶жүҖжңүз®—жі•еҜ№иҪҜ件ејҖеҸ‘е•ҶејҖж”ҫи°ғз”ЁпјҢеҸҜд»Ҙз”ЁжқҘеҒҡеә•еұӮз®—жі•е№іеҸ°гҖӮ
пјҲж•°жҚ®еӨ§и„‘еҗҢж—¶жҸҗдҫӣз®—жі•е•ҶеҹҺжңҚеҠЎпјҢд»»дҪ•дјҷдјҙйғҪеҸҜд»ҘдҪҝз”ЁеӨҡзј–зЁӢиҜӯиЁҖејҖеҸ‘з®—жі•пјҢз”ұеӣҪе·ҘжҷәиғҪиҝӣиЎҢжөӢиҜ•еӣһиҙӯгҖӮпјү
ж•°жҚ®еӨ§и„‘дәәе·ҘжҷәиғҪи®Ўз®—е№іеҸ°иғҢеҗҺжӢҘжңүејәеӨ§зҡ„ж•°жҚ®еҲҶжһҗеӣўйҳҹпјҢжӮЁжҸҗйңҖжұӮжҲ‘们解еҶігҖӮ
е…ҚиҙЈеЈ°жҳҺпјҡеёӮеңәжңүйЈҺйҷ©пјҢйҖүжӢ©йңҖи°Ёж…ҺпјҒжӯӨж–Үд»…дҫӣеҸӮиҖғпјҢдёҚдҪңд№°еҚ–дҫқжҚ®гҖӮ
иҙЈд»»зј–иҫ‘пјҡkj005
ж–Үз« жҠ•иҜүзғӯзәҝ:156 0057 2229 жҠ•иҜүйӮ®з®ұ:29132 36@qq.comдёҖдёӘдё“дёҡзҡ„иөӣдәӢжҺҲжқғдҪ“зі»пјҢиғҪз»ҷз”өз«һдә§дёҡеёҰжқҘеӨҡеӨ§зҡ„д»·еҖјз©әй—ҙ
科жҠҖиғҪеҠӣдёҚж–ӯжҸҗеҚҮ жҲ‘еӣҪж–°дёҖд»ЈиҝҗиҪҪзҒ«з®ӯе°Ҷжү§иЎҢ2022е№ҙйҰ–еҸ‘д»»еҠЎ
еӨ®и§Ҷйў‘з§ҜеҲҶе•ҶеҹҺдёҠзәҝвҖңзҺ°йҮ‘е·Ёжғ вҖқж–°еҠҹиғҪ жҖ»еҸ°ж–ҮеҲӣи¶…еҖјиҙӯ
жӨҚеҸ‘еҖјдёҚеҖјпјҹ专家жҢҮеҮәжӨҚеҸ‘еҸӘжҳҜжІ»з–—зҺҜиҠӮд№ӢдёҖ
вҖңеҸҢеҚғе…ҶвҖқзҪ‘з»ңи®ҫж–Ҫе»әи®ҫеҠ еҝ« зҙҜи®ЎејҖйҖҡ5Gеҹәз«ҷиҫҫ142.5дёҮдёӘ
ж•°еӯ—еҢ–еҲӣж–°еј•йўҶеҸ‘еұ• еҠ еҝ«йҮҠж”ҫж•°еӯ—з»ҸжөҺејәеҠІеҠЁиғҪ
зӣёе…іж–°й—»
жңҖж–°иө„и®Ҝ
科жҠҖжҺЁиҚҗ
- гҖҗдёҡз•ҢгҖ‘ еҠ еҝ«жҸҗеҚҮдә§дёҡеҲӣж–°иғҪеҠӣ е·ҘдёҡжңәеҷЁдәәд»ҚйңҖзҲ¬еқЎиҝҮеқҺ
- гҖҗдёҡз•ҢгҖ‘ иҷҡжӢҹзҺ°е®һжҠҖжңҜдёҚж–ӯжј”иҝӣ иҷҡжӢҹж•°еӯ—дәәеӨ§и§„жЁЎиҗҪең°йқўдёҙдёүеӨ§йҡҫйўҳ
- гҖҗиЎҢдёҡгҖ‘ жҲ‘еӣҪж–°иғҪжәҗжұҪиҪҰдә§дёҡеҝ«йҖҹеҸ‘еұ• иҝһз»ӯ7е№ҙеұ…дё–з•ҢйҰ–дҪҚ
- гҖҗдёҡз•ҢгҖ‘ зҪ‘иҒ”еҢ–гҖҒжҷәиғҪеҢ–жҠҖжңҜеҠ йҖҹжј”иҝӣ жҷәиғҪзҪ‘иҒ”иҪҰиҝӣе…ҘеҚҸеҗҢеҸ‘еұ•е…ій”®жңҹ
- гҖҗдёҡз•ҢгҖ‘ й”ҡе®ҡжңәеҷЁдәәиөӣйҒ“ вҖңжңәеҷЁдәәе·ҘеҸӢвҖқжӯЈжҲҗдёәзҺ°е®һ
- гҖҗдёҡз•ҢгҖ‘ е®һдҪ“йӣ¶е”®дёҡиҪ¬еһӢеҠ йҖҹ ж•°жҷәеҢ–жҲҗйӣ¶е”®дёҡеҸҳйқ©ж–°и¶ӢеҠҝ
科жҠҖеӣҫзүҮ
ж–°й—»жҺ’иЎҢ
- 1
е®№еЈ°WILL SPACEеҶ°з®ұиҚЈиҺ·жңҖдҪіз§‘...
- 2
й«ҳз«Ҝ家з”өеҙӯйңІеӨҙи§’ дәҢжүӢ家з”өдәӨжҳ“еҚҮжё©
- 3
“жҮ’дәә家з”ө”жҲҗеӨ§еҠҝжүҖи¶Ӣ “жҮ’дәә...
- 4
дёҡз»©еӨ§еўһ зҒ«жҳҹдәә2021е№ҙеәҰеҪ’жҜҚеҮҖ...
- 5
дёҡз»©дә®зңј еҢ—йјҺиӮЎд»Ҫ2021е№ҙеәҰеҮҖеҲ©...
- 6
жҷәиғҪ家з”ө“йҖӮиҖҒеҢ–”еҠ йҖҹ иҜӯйҹіжҺ§...
- 7
дә§е“Ғз»“жһ„еҚҮзә§жҳҫи‘— 2021е№ҙжҙ—иЎЈжңә...
- 8
еўһйҖҹиҝ…зҢӣ еҶІзүҷеҷЁеҰӮдҪ•иҝӣдёҖжӯҘвҖңз ҙеұҖвҖқ
- 9
жқҫдёӢжҗәжүӢеӨҡ家еҗҲдҪңдјҒдёҡ еҠ©еҠӣеҢ—дә¬...
- 10
з»Ҳз«ҜеҮәиҙ§йҮҸи¶…1дәҝйғЁпјҒдёӯе…ҙ2021е№ҙ...